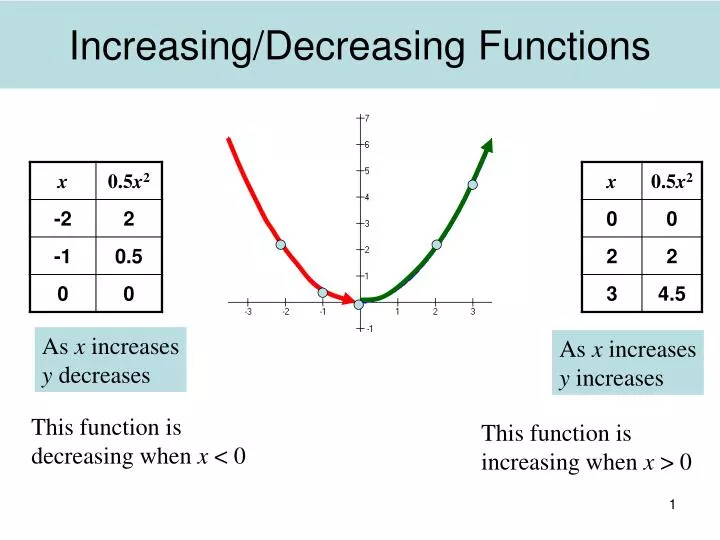
Section 51 The First Derivative Increasing/Decreasing Test (a) If f0(x) > 0onaninterval,thenf is increasing on that interval (b) If f0(x) < 0onaninterval,thenf is decreasing on that interval Definition A critical number of a function f is a number c in the domain of f such that either f0(c)=0orf0(c)doesnotexist 1 Find the critical numbers for f(x)=x2 6xDecreasing on (100) Of®) is decreasing on (0,5);1) If f0(x) > 0 for all x in I, then f is increasing(%) on I 2) If f0(x) < 0 for all x in I, then f is decreasing(&) on I Proof We have proved the flrst result as a corollary of Mean Value Theorem in class Here to remind ourselves MVT we will prove the second one Let f0(x) < 0 on the interval I Pick any two points x1 and x2 in I where x1

Ex 6 2 11 Prove F X X2 X 1 Is Neither Strictly Increasing
F(x)=(x-1)(x-2)^2 increasing or decreasing
F(x)=(x-1)(x-2)^2 increasing or decreasing-If f(x) > 0, then the function is increasing in that particular interval If f(x) < 0, then the function is decreasing in that particular interval Example 1 Find the intervals in which f(x) = 2x³x²x is increasing or decreasing Solution f(x) = 2x 3 x 2 x Step 1 f'(x) = 6x² 2x ÷ by 2 ⇒ 3x²x10 Step 2 f'(x) = 0 determine the intervals over which the function is increasing, decreasing, or constant f(x)=√x^21 Calculus Consider the function f(x)=ln(x)/x^6 For this function there are two important intervals (A,B and B,∞) where A and B are critical numbers or numbers where the function is undefined




Let I Be Any Interval Disjoint From 1 1 Prove That The Function F Given By F X X 1 X Is Strictly Increasing On I Mathematics Shaalaa Com
Figure 335 Number line for f in Example 332 In summary, f is increasing on the set ( − ∞, − 1) ∪ (3, ∞) and is decreasing on the set ( − 1, 1) ∪ (1, 3) Since at x = − 1, the sign of f'\ switched from positive to negative, Theorem 332 states that f( − 1) is a relative maximum of fAnswer Find the intervals on which f ( x) is increasing, the intervals on which f ( x) is decreasing, and the local extrema f ( x) = x ln x − x Calculus for Business, Economics, Life Sciences, and Social Sciences 13th Chapter 4 Graphing and Optimization Section 1 First Derivative and GraphsX Definitions of Increasing and Decreasing Functions A function is increasing on an interval when, for any two numbers and in the interval, implies A function is decreasing on an interval when, for any two numbers and in the interval, implies x 1 < x 2 f x 1 > f x 2 f x 1 x 2 x 1 < x 2 f x 1 < f x 2 f x 1 x 2 THEOREM 35 Test for Increasing
Misc 7 Find the intervals in which the function f given by f (x) = x3 1/𝑥^3 , 𝑥 ≠ 0 is (i) increasing (ii) decreasingf(𝑥) = 𝑥3 1/𝑥3Finding f'(𝒙) f'(𝑥) = 𝑑/𝑑𝑥 (𝑥^3𝑥^(−3) )^ = 3𝑥2 (−3)^(−3 − 1)= 3𝑥2 – 3𝑥^(−4)= 3𝑥^2−3/𝑥^4 = 3(𝑥^2−1/𝑥^4 )Putting f'(𝒙) = 03(𝑥^2− (टीचू) MathsThe function is decreasing over its domain (Note that the function is not defined at x = 0, since division by zero is undefined) That the function increases is apparent from a visual inspection of the graph But one might ask, "Why?" Let's rewrIncreasing on (1,co) OO) is decreasing on (601);
Tap for more steps Set the x − 1 x 1 equal to 0 0 x − 1 = 0 x 1 = 0 Add 1 1 to both sides of the equation x = 1 x = 1 x = 1 x = 1 The equation is undefined where the denominator equals 0 0, the argument of a square root is less than 0 0, or the argument of a Find f'(x) f'(x) = 4 cos (x) sin (x) Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice OA The function is increasing on the open interval(s) ,0U „ and decreasing on the open interval(s) (Simplify your answers On the other hand, if by "itexf/itex is strictly increasing at itexx/itex" you mean "there is an open neighbourhood of itexx/itex on which itexf/itex is strictly increasing" then itexf/itex is not strictly increasing or decreasing at 0 1 If itexX/itex consists of a single point then tex(\forall x \in X)(\forall y




Ex 6 2 6 Find Intervals In Which Functions Strictly Increasing




Find The Intervals In Which F X Log 1 X X 1 X Is Increasing Or Decreasing Maths Application Of Derivatives Meritnation Com
Question 1 Find The Intervals On Which F(x) Is Increasing, Decreasing And Its Local Extrema F(x) = X 3x 2 2 Summarize The Pertinent Information Obtained By Applying Graphing Strategy And Sketch The Graph Of F(x) = 2x X3 3 Use L'Hopital Rule To Find (@2x 1) Xto = – e x(1 – x) (x – 1)(2x 1) f is increasing when f'(x) ≥ 0 and decreasing when f'(x) ≤ 0 Thus f is increasing in –1/2, 1 ∴ f'(x) > 0 f(x) is increasing on (0, 1) Since 0 < x < 157 099 < x99 < (157)99 0 × 100 < 100x99 < (157)99 × 100 0 < 100x99 < (157)99 × 100 Since 0 < x < 𝜋/2 So x is in 1st quadrant ∴ cos x is positive Thus, f(x) is strictly decreasing for none of the intervals So, (D) is the correct answer Show More




Graphs Of Functions Text Example Solutionthe Graph Of F X X Is By Definition The Graph Of Y X We Begin By Setting Up A Partial Table Ppt Download



Find The Intervals In Which The Function F X X 1 3 X 2 2 Is Sarthaks Econnect Largest Online Education Community
F0(x) = 0 when x= 1 and x= 5; 1 determine the interval(s) where the function f(x)= 1 / 2x10 is a) positive b) Increasing 2 Consider the function f(x) = 3 / 4x5 a) Determine the key features of the function i) Domain and range ii)Intercepts iii) EquationsSo, f (x) is increasing on (−∞, 2−1 ∪21 ,∞) (b) For decreasing function, ⇒ x24x2 −1 ≤ 0




Ex 6 2 19 Mcq The Interval In Which Y X2 E X Is Increasing




Solve This Q Find The Intervals In Which The Function F X 3 Log 1 X Maths Application Of Derivatives Meritnation Com
1 This proof is from theorem 140 from Hardy's Inequalities Let f(x) = ln(1 1 x)x = x(ln(x 1) − ln(x)) We refer to the mean value theorem for each differentiable g , g(x h) − g(x) = hg ′ (x θh) for θ ∈ (0, 1) Applying the MVT to g(x) = ln(x), we get ln(x 1) − ln(x) = 1 x θ 2nd PUC Maths Application of Derivatives NCERT Text Book Questions and Answers Ex 62 Question 1 Find the intervals in which the function f given by f (x) = 3x 17 is strictly increasing in R Answer f (x) = 3x 17 f' (x) = 3 > 0 , ∀ x ∈ R hence f (x) is strictly increasingF(x) is an odd function Again f ( x ) = ( e 2 x − 1 e 2 x 1 ) ⇒ f ′ ( x ) = 4 e 2 x ( 1 e 2 x ) 2 > 0 ∀ n ∈ R ⇒ f ( x ) is an increasing function




Find The Intervals In Which F X X 1 X 2 2 Is Increasing Or Decreasing Youtube




Find The Intervals In Which F X 2log X 2 X 2 4x 1 Is Increasing Or Decreasing Maths Application Of Derivatives Meritnation Com
Strictly speaking it is neither f(1)=0 is a constant However, f'(x) = 2(x2)(x1)(x2)^2, so f'(1)=1 Note that f' is continuous near 1 So, f'(x) is positive near 1 and f(x) is increasing near 1 Note For a number a, the phrase "near a" means "in some open interval containing a"If f′(x) > 0, then f is increasing on the interval, and if f′(x) < 0, then f is decreasing on the interval This and other information may be used to show a reasonably accurate sketch of the graph of the function Example 1 For f(x) = x 4 − 8 x 2 determine all intervals where f is increasing or decreasingThe derivative is positive outside of 2,1 and is negative inside of 2,1We can conclude that f is increasing outside of 2,1 and decreasing inside of 2,1The graph is shown below We saw that the values of x such that the derivative is 0 was of special interest




Determine The Values Of X For Which F X X 2 X 1 X 1 Is Increasing Or Decreasing




Increasing And Decreasing Function 1 Strictly Increasing Function
Functions are increasing, decreasing and constant when you plot the graph of the function in a coordinate system Let's define the meaning of these functions Increasing function A function is increasing in an interval for any and if implies Example Let be a function Find all the values for the function to plot the graph xCBSE CBSE (Arts) Class 12 Question Papers 17 Textbook Solutions Important Solutions 24 Question Bank Solutions Concept Increasing and Decreasing Functions video tutorial ;Increasing on (500) None of these The graph of the dermative of a
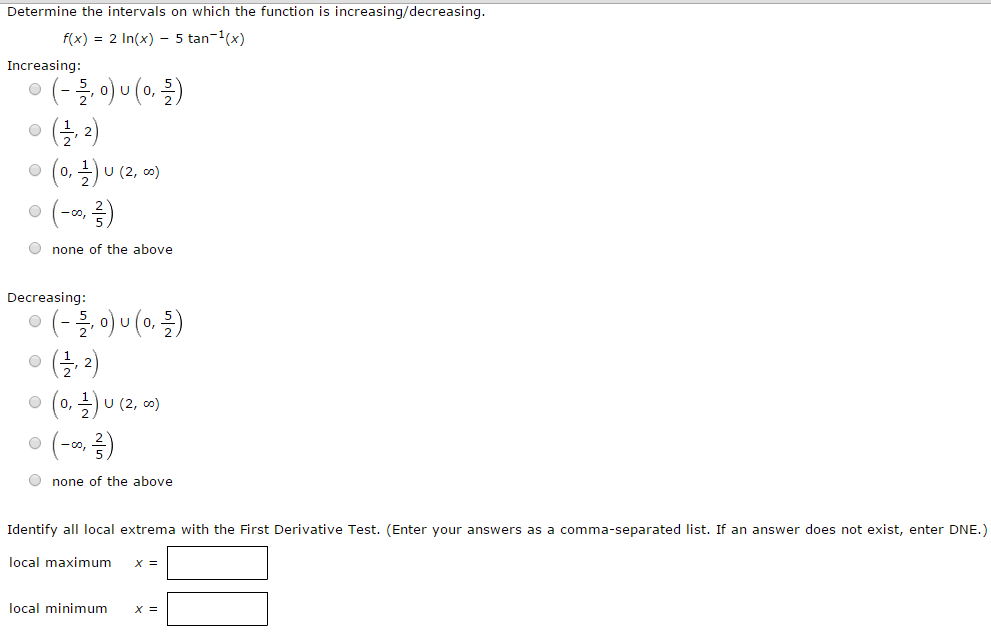



Determine The Intervals On Which The Function Is Chegg Com




Prove That The Function F Given By F X X2 X 1 Is Neither Strictly Increasing Nor Strictly Decreasing On 1 1 Mathematics Shaalaa Com
Select one Of(x) is decreasing on (0,1); `f'(x)=(1x^2)/(x^21)^2` If the resulting value of f'(x) is negative, the function is decreasing in that interval If it is positive, the function is increasingTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find the intervals in which `f(x)=(x1)^3(x2)^2`is increasing or decreasing
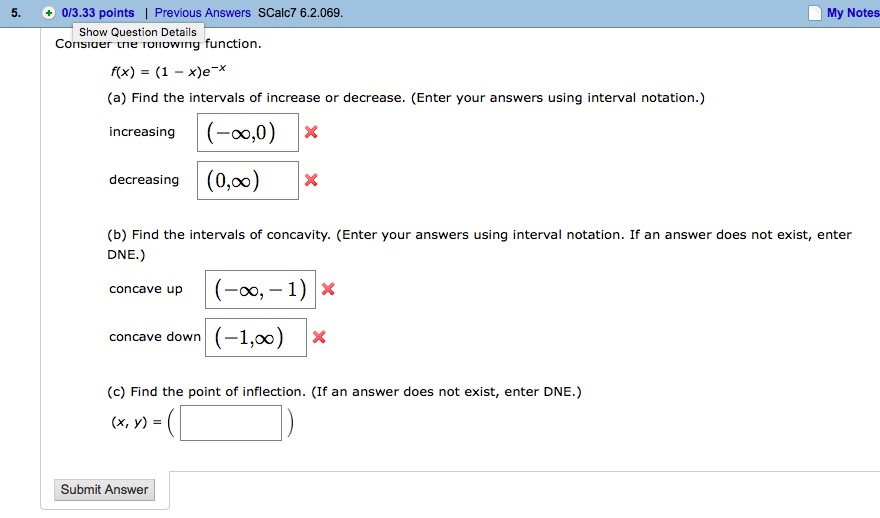



Consider The Following Function F X 1 X E X Chegg Com




Increasing And Decreasing Function 1 Strictly Increasing Function
Test whether the function is increasing or decreasing f(x) = x1x, x ∈ R, x ≠ 0, Maharashtra State Board HSC Science (Computer Science) 12th Board Exam Question Papers 181 Textbook Solutions Online Tests 60 Important Solutions 3532 Question Bank Solutions Get an answer for '`f(x) = (x^2 2x 1)/(x 1)` Find the critical numbers, open intervals on which the function is increasing or decreasing, apply first derivative test toThis video screencast was created with Doceri on an iPad Doceri is free in the iTunes app store Learn more at http//wwwdocericom



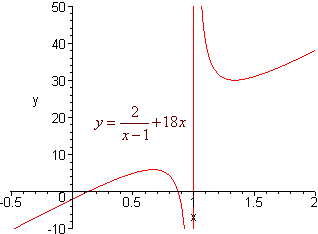
Pslv Soln Rational Functions
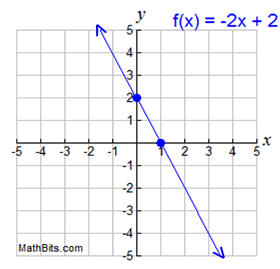



Features Of Function Graphs Mathbitsnotebook A1 Ccss Math
Show that F(X) = E1/X, X ≠ 0 is a Decreasing Function for All X ≠ 0 ?Thus, at the transition (from left to right) through the point \(x = 1\), the function changes from increasing to decreasing, ie \(x = 1\) is the maximum point of the function Similarly, \(x = 3\) is the minimum point of the function Figure 24 Figure 25Increasing on (1c0) OfQ) is increasing on (01);
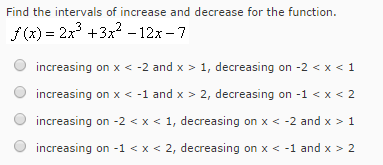



Find The Intervals Of Increase And Decrease For The Chegg Com



Finding The Values Of X When F X Is Increasing Decreasing The Student Room
The total cost C(x) in Rupees associated with the production of x units of an item is given by C(x) = 0007 x – 0003 x 2 15 x 4000 Find the marginal cost when 17 units are produced HereThe first thing to note is that the zeros of the derivative occur at x=1, x=2, and x=3 So, you must select a number on each of the intervals (inf,1), (1,2), (2,3), and (3,inf) to determine if the derivative is positive or negative on that interv 1Answer 1vote answeredby ShrutiBharti(345kpoints) selectedby Vikash Kumar Best answer Given, f(x) = (x 1)3 (x 2)2 On differentiating both sides wrt x, we get Now, we find intervals and check in which interval f(x) is strictly increasing and strictly decreasing



Increasing And Decreasing Functions



Increasing And Decreasing Functions
Find the intervals where f is increasing and decreasing if f(x) = (1/5)x^5 Analyzing Functions In order to analyze where does a function is increasing, decreasing, or constant, we have to graphSolution for If ø(x) =(x) f(1x) and f"(x)A) 2 < 0 for t > 0, so g ( t) < 1 for t > 0 Using simple algebra it is possible to prove that g ( x) = f ( 1 / x) = a x − 1 x is strictly increasing for x > 0, a > 0, a ≠ 1 and x being rational The extension to irrational values of x is easily done by considering sequences of rationals converging to x




Increasing Decreasing Functions A Function F Is Increasing On An Interval If For Any X 1 And X 2 In The Interval X 1 X 2 Implies F X 1 F X Ppt Download
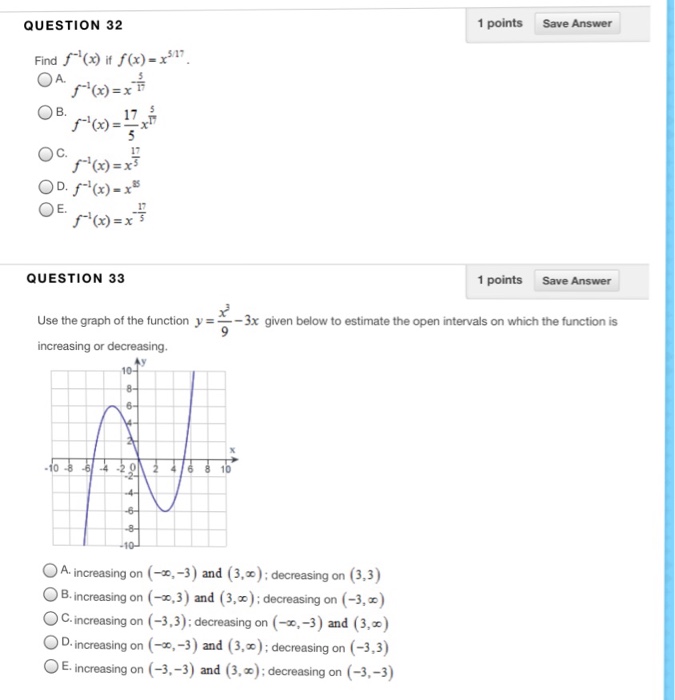



Find F 1 X If F X X 5 17 A F 1 X X Chegg Com
Hence, f′(x) >0 f ′ ( x) > 0 in the interval (−∞,0) ( − ∞, 0) so, the function is increasing in the interval (−∞,0) ( − ∞, 0) Substitute x = 1 x = 1 in the firstorderFind the intervals in which the function f (x) = 4 x 4 − x 3 − 5 x 2 2 4 x 1 2 is (a) strictly increasing, (b) strictly decreasing Medium View solutionPopular Problems Calculus Find Where Increasing/Decreasing f (x)=x1/x f (x) = x 1 x f ( x) = x 1 x Find the derivative Tap for more steps Differentiate Tap for more steps By the Sum Rule, the derivative of x 1 x x 1 x with respect to x x is d d x x d d x 1 x d d x x d d x 1 x




Intervals In Which Function Is Increasing Or Decreasing Problem Example 1 Youtube




Ex 6 2 11 Prove F X X2 X 1 Is Neither Strictly Increasing
F0(x) DNE when x= 7 For problems 715, calculate each of the following (a) The intervals on which f(x) is increasing (b) The intervals on which f(x) is decreasing (c) The intervals on which f(x) is concave up (d) The intervals on which f(x) is concave down (e) All points of in ection Express each as an orderedIf f'(x) = (x 1)e, which of the following statements is true about the function J?




41 Increasing And Decreasing Functions Pdf Calculus Mathematical Objects



Http Euler Fd Cvut Cz Predmety Calculus1en Cal1 Soubory Files Exercises Monotony Pdf




23 The Graph Of F X 1 2 1 X X 2 X 2 Is Chegg Com



Q Tbn And9gcqfhuxhmizntsns V1x7khz5m A5m8vqbqk2v3lmpebzl 5tjrm Usqp Cau



Classxii Sub Mathematics Topic Increasing Decreasing Increasing Decreasing




Let I Be Any Interval Disjoint From 1 1 Prove That The Function F Given By F X X 1 X Is Strictly Increasing On I Mathematics Shaalaa Com
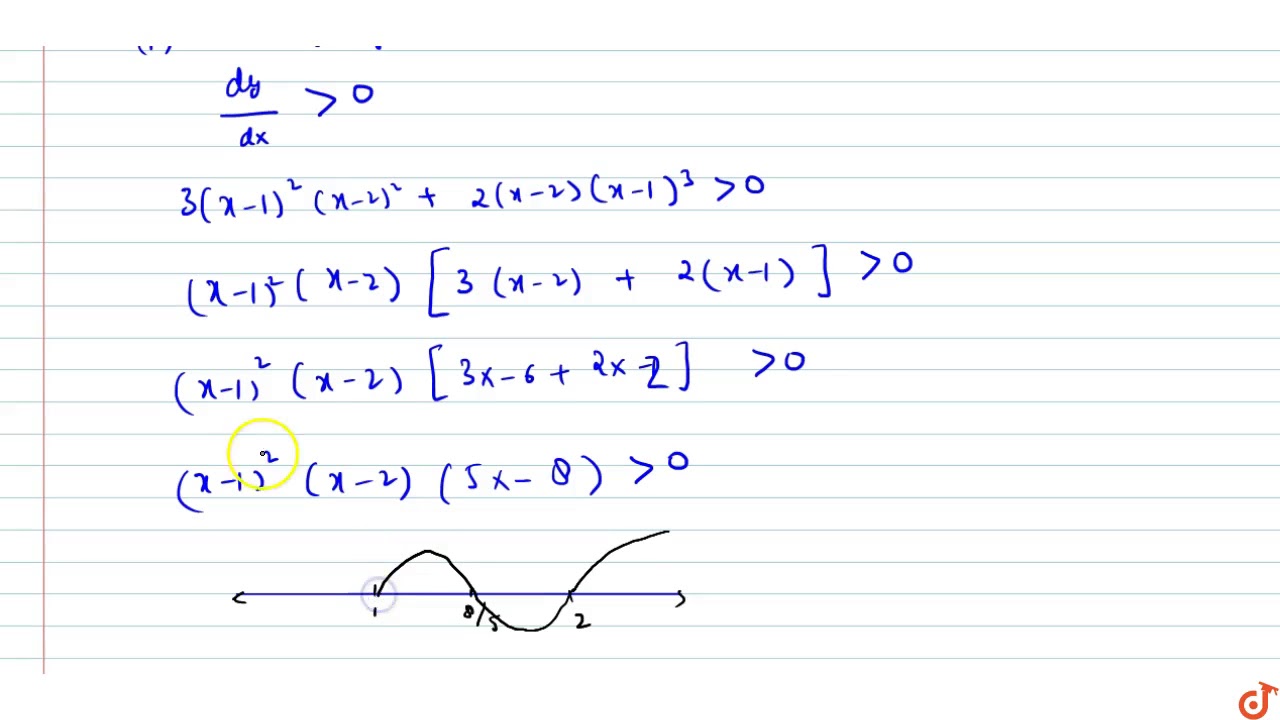



Find The Intervals In Which F X X 1 3 X 2 2 Is Increasing Or Decreasing Youtube




Find The Intervals In Which F X 4x 2 1 X Is Increasing Or Decreasing
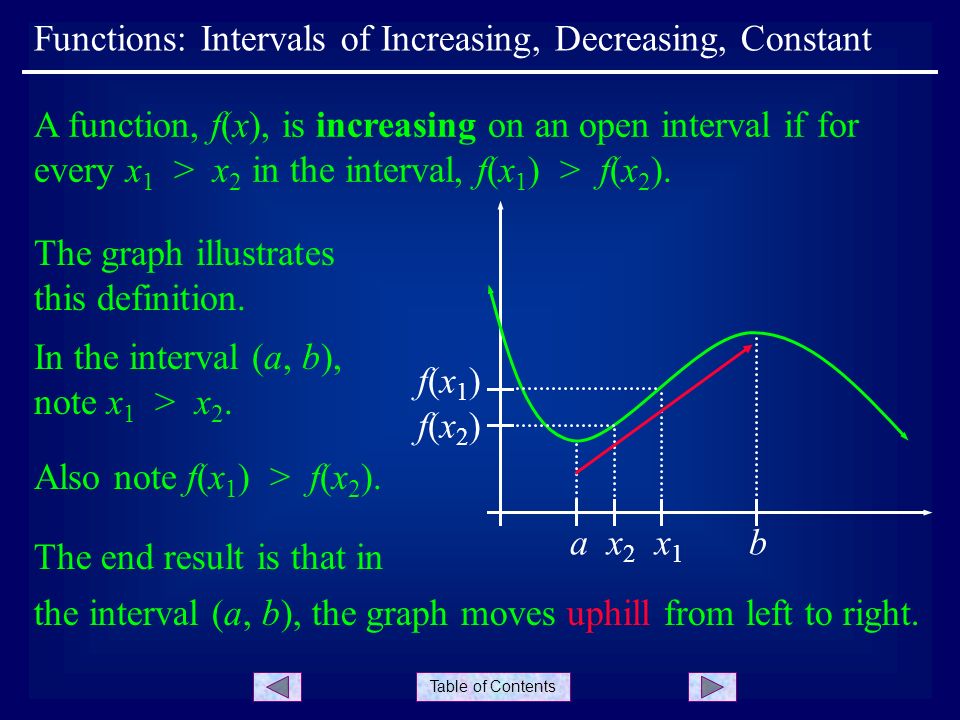



Table Of Contents Functions Intervals Of Increasing Decreasing Constant A Function F X Is Increasing On An Open Interval If For Every X 1 X 2 In Ppt Download



Increasing Decreasing Functions Examples



1
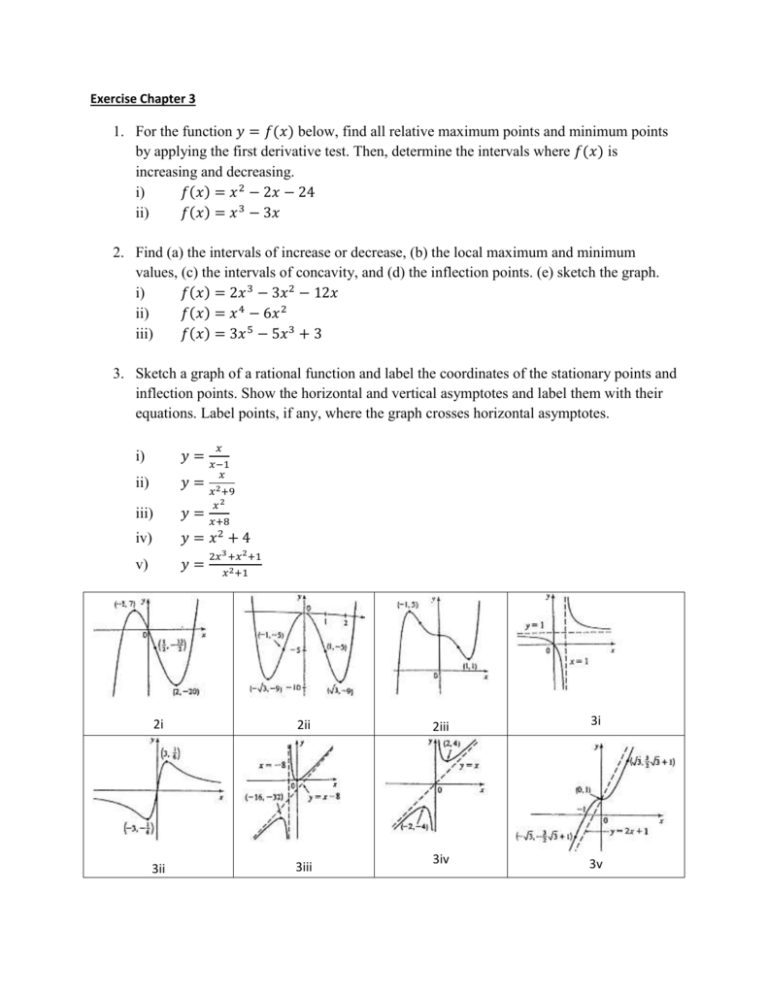



Exercise Chapter 3 Mathcfs Students Page




Show That F X 1 X Is A Decreasing Function On 0 Oo




Classxii Sub Mathematics Topic Increasing Decreasing Increasing Decreasing
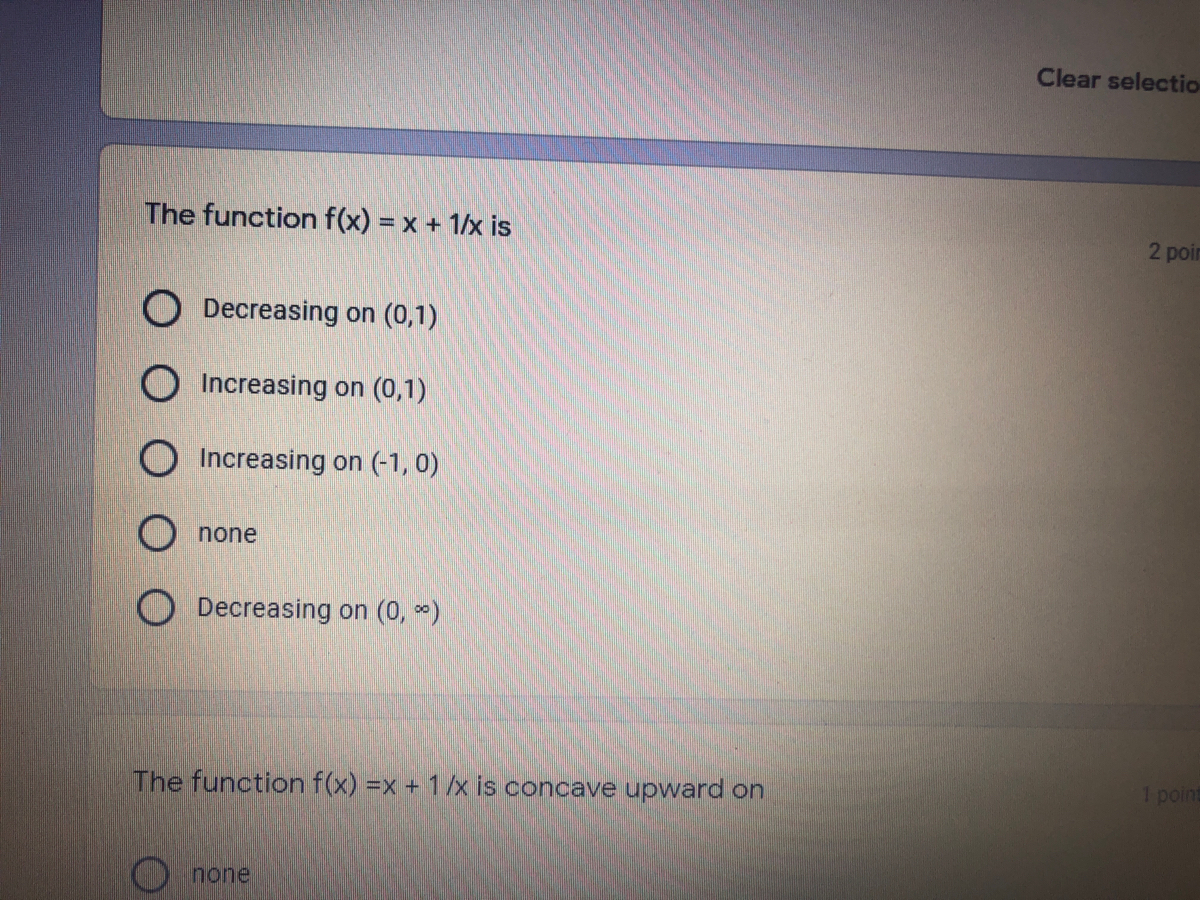



Answered The Function F X X 1 X Is 2p O Bartleby




Misc 7 Find Intervals F X X3 1 X3 X 0 Is Increasing




Calc 1 Pod 43 Find The Intervals On Which F Is Increasing And Decreasing F X X 2 Ln X 2 2 Youtube



Determine For What Values Of X The Function F X X 3 1 X 3 X 0 Is Strictly Increasing Or Strictly Decreasing Sarthaks Econnect Largest Online Education Community



Www Hoodriver K12 Or Us Cms Lib Or Centricity Domain 230 Ch 5 pt answer key Pdf




A Find The Intervals In Which The Function F X Log 1 X X 1 X Is I Increasing Ii Decreasing Function B Find The Intervals In Which The Function F X X Log E X X Gt 0 Is Increasing Or Decreasing




Determine The Values Of X For Which F X X 2 X 1 X 1 Is Increasing Or Decreasing
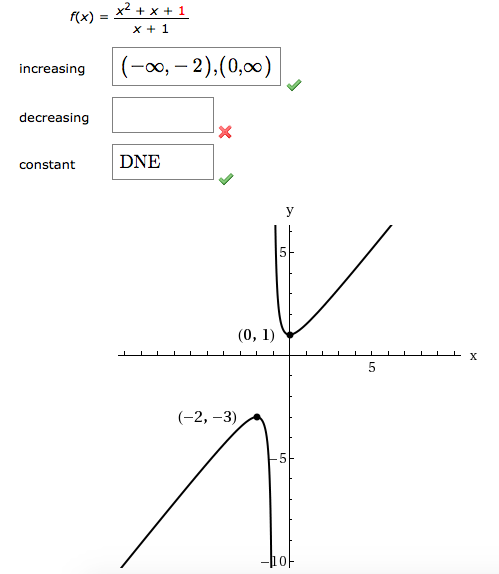



Determine The Intervals On Which The Function Is Chegg Com




Classxii Sub Mathematics Topic Increasing Decreasing Increasing Decreasing
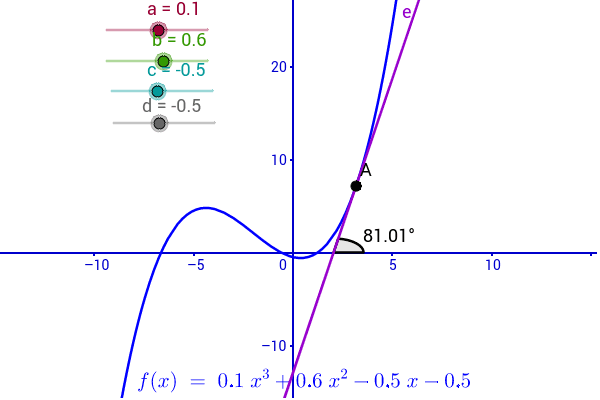



Increasing And Decreasing Function Geogebra



Http Www Mast Queensu Ca Math121 Assignments Unit06 Pdf




View Question Properties Of This Reciprocal Function F X X 1 X 1



Increasing And Decreasing Functions



Math Scene Functions 2 Lesson 2




Find The Interval On Which The Following Function Is A Strictly Increasing B Strictly Decreasing F X 3x 4 4x 3 12x 2 5




Find The Intervals In Which F X X 1 3 X 2 2 Is Strictly Increasing And Strictly Decreasing Brainly In




1 Sinx In 9 1 In The Interval 1 0 X 5 2 7



Joerg Endrullis




Is The Function F X Increasing Or Decreasing Over The Interval 2 Lt X Lt 1 Brainly Com



Find The Intervals In Which The Function F X X 1 3 X 2 2 Is Sarthaks Econnect Largest Online Education Community
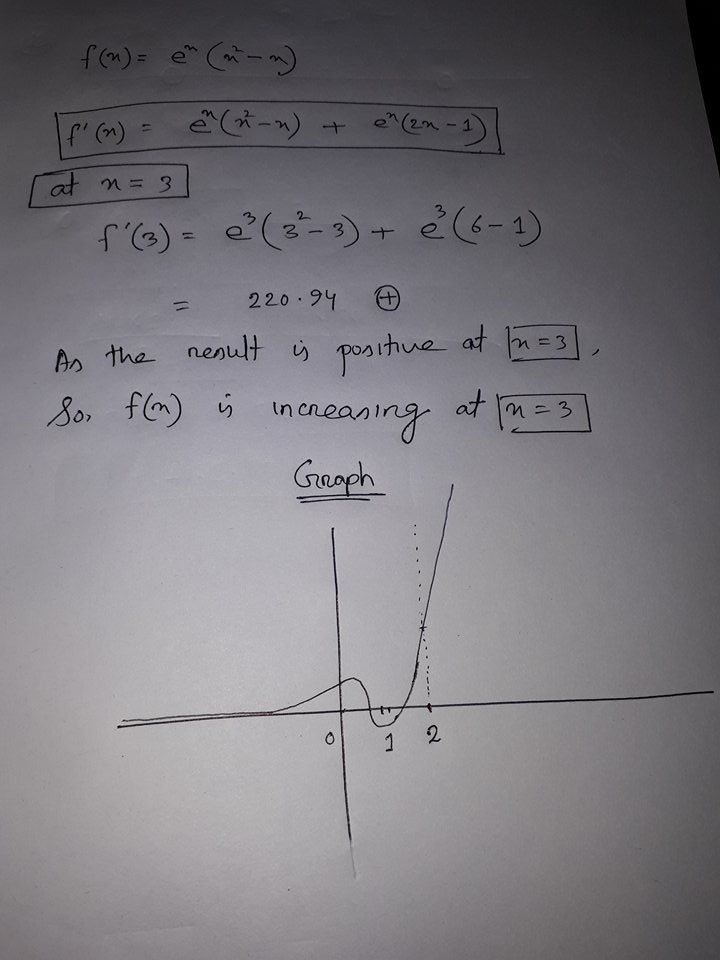



Is F X E X X 2 X Increasing Or Decreasing At X 3 Socratic




The Graph Of The Function F X X 4 X 1 Is Shown Below Which Statement About The Function Is Brainly Com
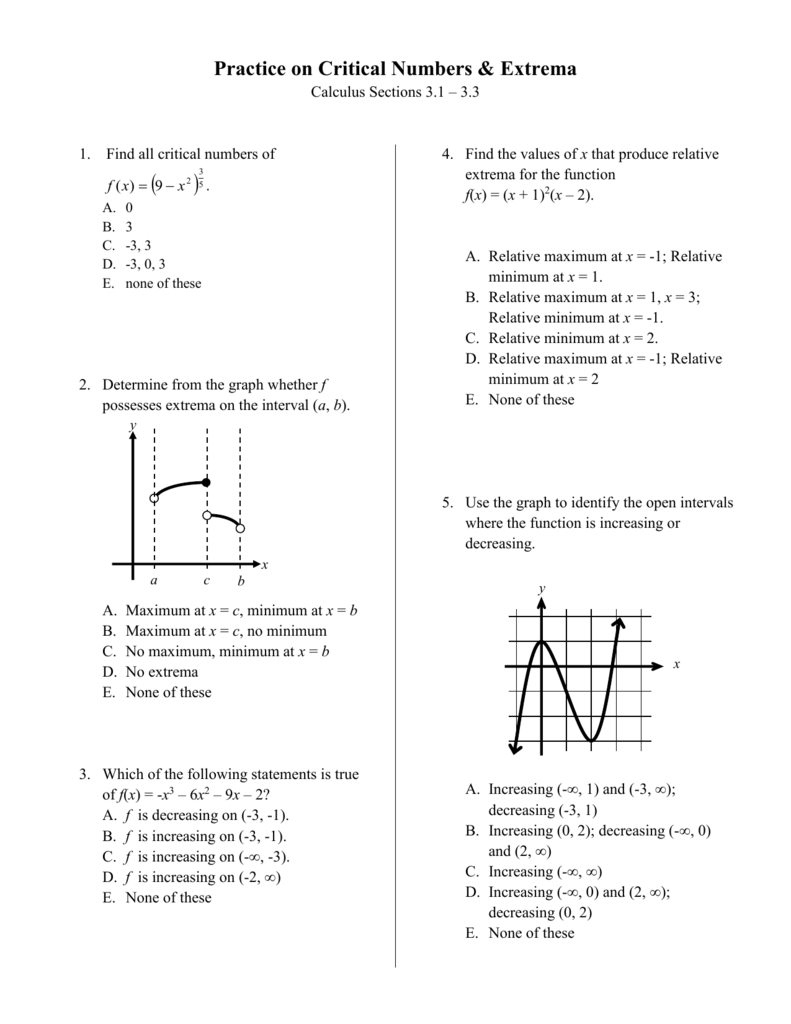



Practice On Critical Numbers Extrema




X 1x Is Increasing On 1



Http Www Math Tamu Edu Mayaj Chapter5 Sec5p1completed Pdf



Increasing And Decreasing Functions
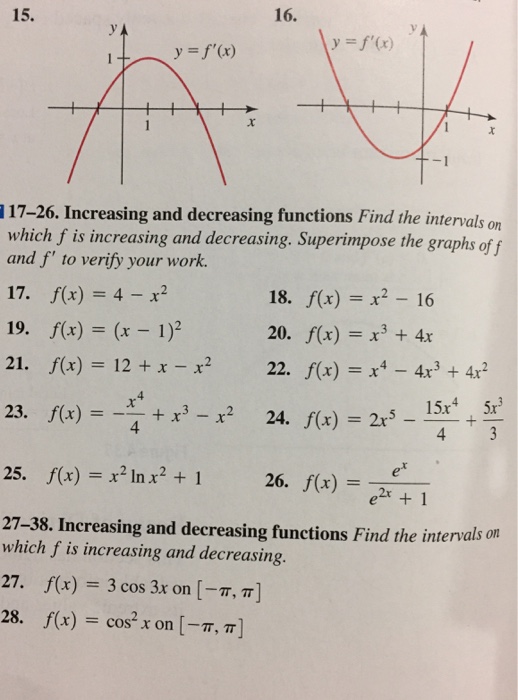



Increasing And Decreasing Functions Find The Chegg Com



Find The Intervals Of Increasing And Or Decreasing Chegg Com




Find The Intervals In Which F X X 1 X 3 Is 1 Strictly Increasing 2 Strictly Decreasing Brainly In




F R Gt R F X X 1 X 2 Determine Intervals In Which The Given Function Are Strictly Increasing Or Brainly In



Ppt Increasing Decreasing Functions Powerpoint Presentation Free Download Id




5 3 A Curve Sketching Ppt Video Online Download



Increasing Decreasing Ppt Video Online Download




Rd Sharma Class 12 Solutions Chapter 17 Increasing And Decreasing Functions




The Function F X X 2 2x 5 Is Strictly Increasing In The Interval



Find The Intervals In Which The Function F X Log 1 X X 1 X Is Strictly Increasing Sarthaks Econnect Largest Online Education Community



Increasing Decreasing Functions Examples



Ppt Increasing Powerpoint Presentation Free Download Id




Misc 7 Find Intervals F X X3 1 X3 X 0 Is Increasing




Ex 6 2 11 Prove F X X2 X 1 Is Neither Strictly Increasing




Rd Sharma Class 12 Solutions Chapter 17 Increasing And Decreasing Functions
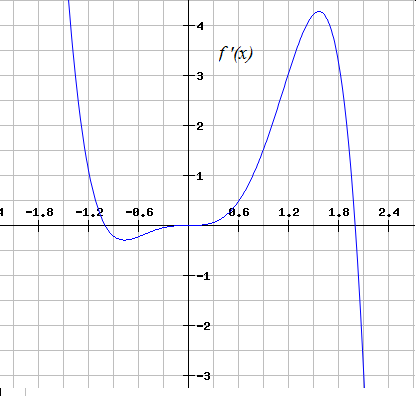



How To Find Increasing Intervals By Graphing Functions Calculus 1
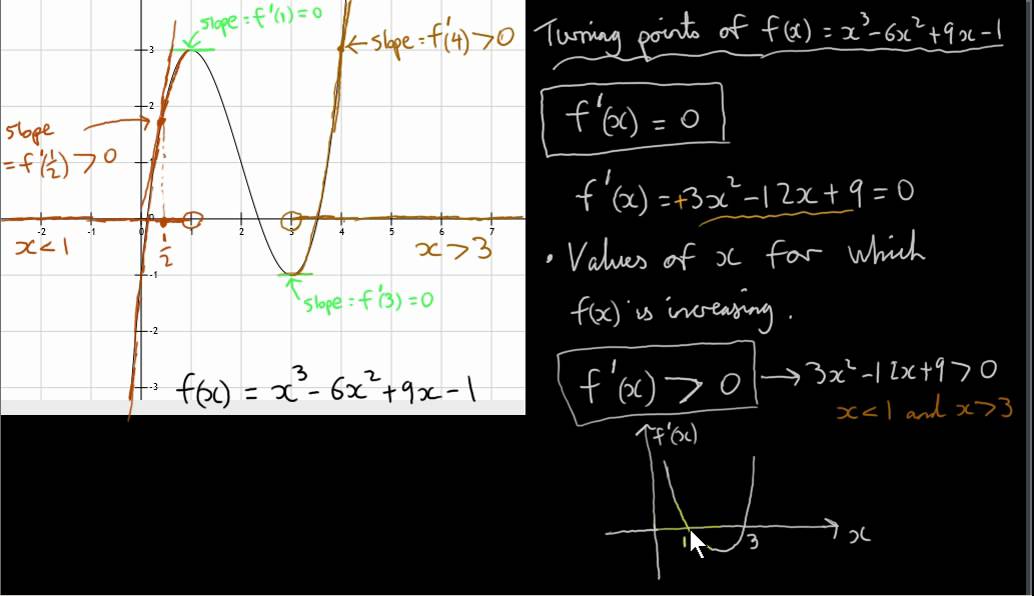



How To Find The Values Of X For Increasing And Decreasing F X Youtube
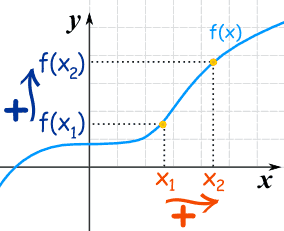



Increasing And Decreasing Functions
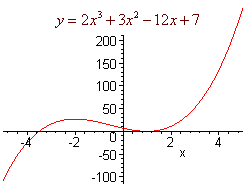



Increasing And Decreasing Functions




Intervals On Which A Function Is Increasing Chegg Com




How To Find Increasing And Decreasing Interval For Continuous Rational Function Youtube




Show That F X 1 1 X 2 Is Neither Increasing Nor Decreasing On R




Ex 6 2 6 Find Intervals In Which Functions Strictly Increasing




Find The Intervals In Which The Function F X Log 1 X Frac 2 X 2 X Is Strictly Increasing Or Decreasing




Answered 3 3 Increasing And Decreasing Functions Bartleby




Find The Intervals In Which The Function F X X 4 X 3 3 Is Increasing Or Decreasing
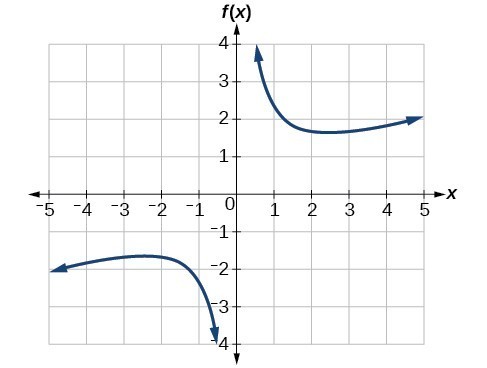



Use A Graph To Determine Where A Function Is Increasing Decreasing Or Constant College Algebra




Let F X E X 1 X 1 X N N Where N In N Show That F Is Non Increasing On 0 Infinity Study Com
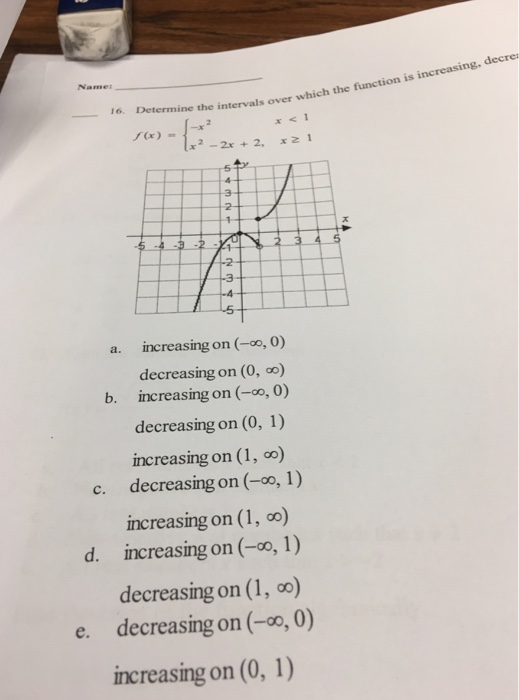



Determine The Intervals Over Which The Function Is Chegg Com



Q Tbn And9gcr1awjnfievvbxtiltp6vsfzl Yvhcce0yraat7t Hr3 P37lem Usqp Cau




Increasing And Decreasing Function 1 Strictly Increasing Function



Day15




Find The Intervals In Which The Function F Given By F X X 3 1 X 3 X 0 Is Mathematics Shaalaa Com




X Log X Increases In The Interval F X X Log X Increases In The Interval F X X Log X Decreases Youtube




Determine For What Values Of X The Function F X X 3 1 X 3 X 0 Is Strictly Increasing Or Strictly Decreasing
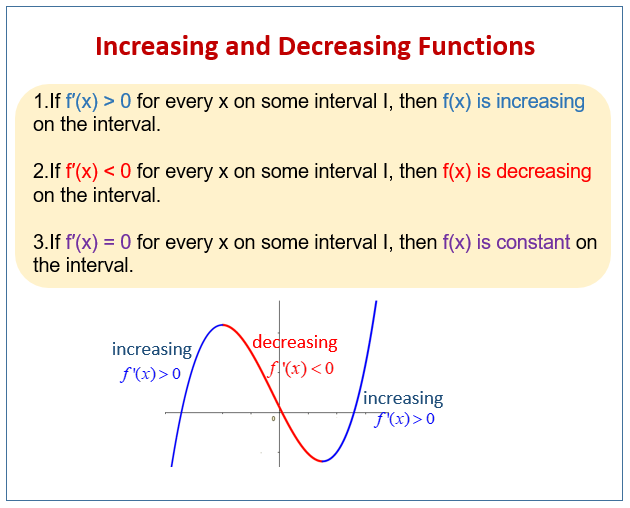



Increasing And Decreasing Functions Examples Solutions Worksheets Videos Activities



Increasing And Decreasing Functions
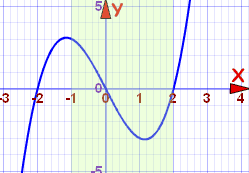



Increasing And Decreasing Functions




Answered 1 For The Function F X X 1 E A Bartleby



Q Tbn And9gcsmm4ktmxrxm10kmsg3wqo5rzire Ogwbm0v2tajixhbesgniod Usqp Cau



0 件のコメント:
コメントを投稿